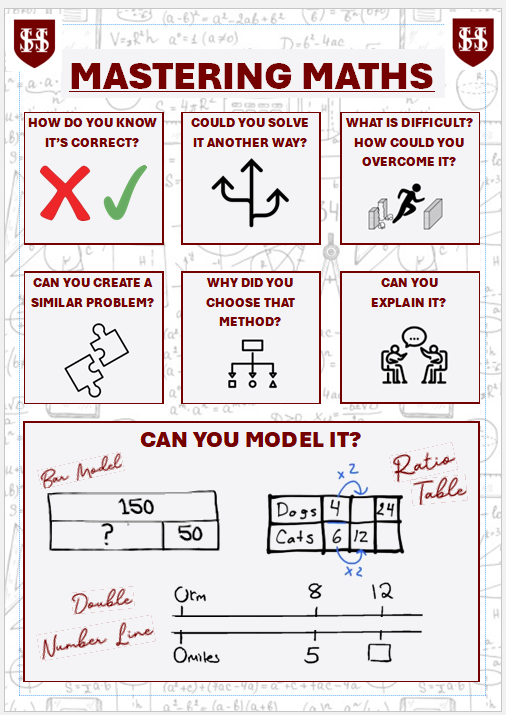
Syllabus:

At Sheringham High School we have developed our scheme of work to form a connected sequence of topics from their starting point in year 7 to the rigours of exam questions at GCSE and beyond. As students progress through the scheme, each topic is built upon
and links are forged between the topics, creating strong foundations for future study. At Sheringham we embrace a mastery approach to our learning, ensuring that the objectives covered for each topic are selected to consolidate students’ prior learning whilst
prioritising stretch and challenge for every student. This approach has allowed us to create a highly differentiated curriculum promoting student progress in every lesson.

Our Scheme of work covers the same areas of Maths tested at GCSE: Number; Algebra; Ratio, Proportion and rates of Change; Geometry and Measures; Statistics and Probability. Our lessons prioritise problem solving methods and real-life applications of the topics
that we study.

At Sheringham our team is very enthusiastic about Maths and we aim to inspire our love of Mathematics in our students and equip them with the mathematical knowledge to succeed in their adult lives.

Assessment

Our students are set from the first lesson in Year 7 based on the Key Stage 2 SATs data. We quickly retest students in September to ensure that we have placed them in the appropriate teaching set and from this, we also build up a picture of their strengths
and areas for development enabling us to create a bespoke approach to the curriculum for each class.

Students will sit a fully assessed paper every half term. The papers at each half term break will be set using all the topics that students have seen so far in their mathematical career. The paper at the end of each term will be set on the topics that students
have covered in the preceding term. These assessments will be marked by teaching staff using our RAS policy.

Sidney in Year 7 achieved a Gold award in the Maths challenge and admission into the next round of the Maths challenge. 

School Certification for participation in the follow-on rounds of the Junior Maths Challenge. 

Our Syllabus at Key Stage 4 builds upon the foundations laid in Key Stage 3. Our syllabus is split into Higher tier (Grades 4-9) and Foundation Tier (Grades 1-5) however, in keeping with our bespoke approach in Key Stage 3, our team will pick the most appropriate objectives for each class from the two schemes of work and the final decision of which tier to sit will be made in year 11. At Sheringham High we have chosen the AQA exam board for our Maths GCSE. Our top set in year 11 also have the opportunity to sit the AQA further Maths qualification.

Assessment

In addition to whole school mock exams, students in year 10 and 11 will sit a series of mini past papers using the associated grade boundaries. These papers will enable students to refine their exam techniques and give them an insight to the range and style
of questions that can be asked at GCSE.

The course is examined with three terminal exams in year 11, one non - calculator paper and two calculator papers. Each exam lasts for 90 minutes and is worth 80 marks. The most significant change to the syllabus is the removal of most of the formulae from
the formula sheet. These need to be remembered and will form a focal point for revision lessons.

Students greatly benefit from having their own calculator to use in the exams and we particularly recommend calculators with a two-line (fraction) function. If you are in any doubt, please contact a member of the Maths team.

For information of courses in Years 12 and 13 click on this link >